Maths researchers hail breakthrough in applications of artificial intelligence

For the first time, computer scientists and mathematicians have used artificial intelligence to help prove or suggest new mathematical theorems in the complex fields of knot theory and representation theory.
The astonishing results have been published today in the pre-eminent scientific journal, Nature.
Professor Geordie Williamson is Director of the University of Sydney Mathematical Research Institute and one of the world's foremost mathematicians. As a co-author of the paper, he applied the power of Deep Mind's AI processes to explore conjectures in his field of speciality, representation theory.
His co-authors were from DeepMind—the team of computer scientists behind AlphaGo, the first computer program to successfully defeat a world champion in the game of Go in 2016.
Professor Williamson said: "Problems in mathematics are widely regarded as some of the most intellectually challenging problems out there.
"While mathematicians have used machine learning to assist in the analysis of complex data sets, this is the first time we have used computers to help us formulate conjectures or suggest possible lines of attack for unproven ideas in mathematics."
Proving mathematical conjectures
Professor Williamson is a globally recognized leader in representation theory, the branch of mathematics that explores higher dimensional space using linear algebra.
In 2018 he was elected the youngest living Fellow of the Royal Society in London, the world's oldest and arguably most prestigious scientific association.
"Working to prove or disprove longstanding conjectures in my field involves the consideration of, at times, infinite space and hugely complex sets of equations across multiple dimensions," Professor Williamson said.
While computers have long been used to generate data for experimental mathematics, the task of identifying interesting patterns has relied mainly on the intuition of the mathematicians themselves.
That has now changed.
Professor Williamson used DeepMind's AI to bring him close to proving an old conjecture about Kazhdan-Lusztig polynomials, which has been unsolved for 40 years. The conjectures concern deep symmetry in higher dimensional algebra.
Co-authors Professor Marc Lackeby and Professor András Juhász from the University of Oxford have taken the process a step further. They discovered a surprising connection between algebraic and geometric invariants of knots, establishing a completely new theorem in mathematics.
In knot theory, invariants are used to address the problem of distinguishing knots from each other. They also help mathematicians understand properties of knots and how this relates to other branches of mathematics.
While of profound interest in its own right, knot theory also has myriad applications in the physical sciences, from understanding DNA strands, fluid dynamics and the interplay of forces in the Sun's corona.
Professor Juhász said: "Pure mathematicians work by formulating conjectures and proving these, resulting in theorems. But where do the conjectures come from?
"We have demonstrated that, when guided by mathematical intuition, machine learning provides a powerful framework that can uncover interesting and provable conjectures in areas where a large amount of data is available, or where the objects are too large to study with classical methods."
Professor Lackeby said: "It has been fascinating to use machine learning to discover new and unexpected connections between different areas of mathematics. I believe that the work that we have done in Oxford and in Sydney in collaboration with DeepMind demonstrates that machine learning can be a genuinely useful tool in mathematical research."
Lead author from DeepMind, Dr. Alex Davies, said: "We think AI techniques are already sufficiently advanced to have an impact in accelerating scientific progress across many different disciplines. Pure maths is one example and we hope that this Nature paper can inspire other researchers to consider the potential for AI as a useful tool in the field."
Professor Williamson said: "AI is an extraordinary tool. This work is one of the first times it has demonstrated its usefulness for pure mathematicians, like me."
"Intuition can take us a long way, but AI can help us find connections the human mind might not always easily spot."
The authors hope that this work can serve as a model for deepening collaboration between fields of mathematics and artificial intelligence to achieve surprising results, leveraging the respective strengths of mathematics and machine learning.
"For me these findings remind us that intelligence is not a single variable, like an IQ number. Intelligence is best thought of as a multi-dimensional space with multiple axes: academic intelligence, emotional intelligence, social intelligence," Professor Williamson said.
"My hope is that AI can provide another axis of intelligence for us to work with, and that this new axis will deepen our understanding of the mathematical world."
More information: Alex Davies, Advancing mathematics by guiding human intuition with AI, Nature (2021). DOI: 10.1038/s41586-021-04086-x. www.nature.com/articles/s41586-021-04086-x
Journal information: Nature
Provided by University of Sydney

Mathematical discoveries take intuition and creativity – and now a little help from AI
Research in mathematics is a deeply imaginative and intuitive process. This might come as a surprise for those who are still recovering from high-school algebra.
What does the world look like at the quantum scale? What shape would our universe take if we were as large as a galaxy? What would it be like to live in six or even 60 dimensions? These are the problems that mathematicians and physicists are grappling with every day.
To find the answers, mathematicians like me try to find patterns that relate complicated mathematical objects by making conjectures (ideas about how those patterns might work), which are promoted to theorems if we can prove they are true. This process relies on our intuition as much as our knowledge.
Over the past few years I’ve been working with experts at artificial intelligence (AI) company DeepMind to find out whether their programs can help with the creative or intuitive aspects of mathematical research. In a new paper published in Nature, we show they can: recent techniques in AI have been essential to the discovery of a new conjecture and a new theorem in two fields called “knot theory” and “representation theory”.
Get your news from people who know what they’re talking about.Sign up for newsletter
Machine intuition
Where does the intuition of a mathematician come from? One can ask the same question in any field of human endeavour. How does a chess grandmaster know their opponent is in trouble? How does a surfer know where to wait for a wave?
The short answer is we don’t know. Something miraculous seems to happen in the human brain. Moreover, this “miraculous something” takes thousands of hours to develop and is not easily taught

The AlphaGo software’s defeat of Lee Sedol in 2016 is regarded as one of the most striking early examples of a machine displaying something like human intuition.
The past decade has seen computers display the first hints of something like human intuition. The most striking example of this occurred in 2016, in a Go match between DeepMind’s AlphaGo program and Lee Sedol, one of the world’s best players.
AlphaGo won 4–1, and experts observed that some of AlphaGo’s moves displayed human-level intuition. One particular move (“move 37”) is now famous as a new discovery in the game.
Read more: AI has beaten us at Go. So what next for humanity?
How do computers learn?
Behind these breakthroughs lies a technique called deep learning. On a computer one builds a neural network – essentially a crude mathematical model of a brain, with many interconnected neurons.
At first, the network’s output is useless. But over time (from hours to even weeks or months), the network is trained, essentially by adjusting the firing rates of the neurons.
Such ideas were tried in the 1970s with unconvincing results. Around 2010, however, a revolution occurred when researchers drastically increased the number of neurons in the model (from hundreds in the 1970s to billions today).

One of the first neural networks, the Mark I Perceptron, was built in the 1950s. The goal was to classify digital images, but results were disappointing. Cornell University
Traditional computer programs struggle with many tasks humans find easy, such as natural language processing (reading and interpreting text), and speech and image recognition.
With the deep learning revolution of the 2010s, computers began performing well on these tasks. AI has essentially brought vision and speech to machines.
Training neural nets requires huge amounts of data. What’s more, trained deep learning models often function as “black boxes”. We know they often give the right answer, but we usually don’t know (and can’t ascertain) why.

A lucky encounter
My involvement with AI began in 2018, when I was elected a Fellow of the Royal Society. At the induction ceremony in London I met Demis Hassabis, chief executive of DeepMind.
Over a coffee break we discussed deep learning, and possible applications in mathematics. Could machine learning lead to discoveries in mathematics, like it had in Go?
This fortuitous conversation led to my collaboration with the team at DeepMind.

Mathematicians like myself often use computers to check or perform long computations. However, computers usually cannot help me develop intuition or suggest a possible line of attack. So we asked ourselves: can deep learning help mathematicians build intuition?
With the team from DeepMind, we trained models to predict certain quantities called Kazhdan-Lusztig polynomials, which I have spent most of my mathematical life studying.
In my field we study representations, which you can think of as being like molecules in chemistry. In much the same way that molecules are made of atoms, the make up of representations is governed by Kazhdan-Lusztig polynomials.
Amazingly, the computer was able to predict these Kazhdan-Lusztig polynomials with incredible accuracy. The model seemed to be onto something, but we couldn’t tell what.
However, by “peeking under the hood” of the model, we were able to find a clue which led us to a new conjecture: that Kazhdan-Lusztig polynomials can be distilled from a much simpler object (a mathematical graph).
This conjecture suggests a way forward on a problem that has stumped mathematicians for more than 40 years. Remarkably, for me, the model was providing intuition!
Read more: How explainable artificial intelligence can help humans innovate
In parallel work with DeepMind, mathematicians Andras Juhasz and Marc Lackenby at the University of Oxford used similar techniques to discover a new theorem in the mathematical field of knot theory. The theorem gives a relation between traits (or “invariants”) of knots that arise from different areas of the mathematical universe.
Our paper reminds us that intelligence is not a single variable, like the result of an IQ test. Intelligence is best thought of as having many dimensions.
My hope is that AI can provide another dimension, deepening our understanding of the mathematical world, as well as the world in which we live.
Professor of Mathematics, University of Sydney
Disclosure statement
Geordie Williamson is a Professor at the University of Sydney, and a consultant in Pure Mathematics for DeepMind, a subsidiary of Alphabet.
Advancing mathematics by guiding human intuition with AI
Nature 600, 70–74 (2021)
Abstract
The practice of mathematics involves discovering patterns and using these to formulate and prove conjectures, resulting in theorems. Since the 1960s, mathematicians have used computers to assist in the discovery of patterns and formulation of conjectures1, most famously in the Birch and Swinnerton-Dyer conjecture2, a Millennium Prize Problem3. Here we provide examples of new fundamental results in pure mathematics that have been discovered with the assistance of machine learning—demonstrating a method by which machine learning can aid mathematicians in discovering new conjectures and theorems. We propose a process of using machine learning to discover potential patterns and relations between mathematical objects, understanding them with attribution techniques and using these observations to guide intuition and propose conjectures. We outline this machine-learning-guided framework and demonstrate its successful application to current research questions in distinct areas of pure mathematics, in each case showing how it led to meaningful mathematical contributions on important open problems: a new connection between the algebraic and geometric structure of knots, and a candidate algorithm predicted by the combinatorial invariance conjecture for symmetric groups4. Our work may serve as a model for collaboration between the fields of mathematics and artificial intelligence (AI) that can achieve surprising results by leveraging the respective strengths of mathematicians and machine learning.
Main
One of the central drivers of mathematical progress is the discovery of patterns and formulation of useful conjectures: statements that are suspected to be true but have not been proven to hold in all cases. Mathematicians have always used data to help in this process—from the early hand-calculated prime tables used by Gauss and others that led to the prime number theorem5, to modern computer-generated data1,5 in cases such as the Birch and Swinnerton-Dyer conjecture2. The introduction of computers to generate data and test conjectures afforded mathematicians a new understanding of problems that were previously inaccessible6, but while computational techniques have become consistently useful in other parts of the mathematical process7,8, artificial intelligence (AI) systems have not yet established a similar place. Prior systems for generating conjectures have either contributed genuinely useful research conjectures9 via methods that do not easily generalize to other mathematical areas10, or have demonstrated novel, general methods for finding conjectures11 that have not yet yielded mathematically valuable results.
AI, in particular the field of machine learning12,13,14, offers a collection of techniques that can effectively detect patterns in data and has increasingly demonstrated utility in scientific disciplines15. In mathematics, it has been shown that AI can be used as a valuable tool by finding counterexamples to existing conjectures16, accelerating calculations17, generating symbolic solutions18 and detecting the existence of structure in mathematical objects19. In this work, we demonstrate that AI can also be used to assist in the discovery of theorems and conjectures at the forefront of mathematical research. This extends work using supervised learning to find patterns20,21,22,23,24 by focusing on enabling mathematicians to understand the learned functions and derive useful mathematical insight. We propose a framework for augmenting the standard mathematician’s toolkit with powerful pattern recognition and interpretation methods from machine learning and demonstrate its value and generality by showing how it led us to two fundamental new discoveries, one in topology and another in representation theory. Our contribution shows how mature machine learning methodologies can be adapted and integrated into existing mathematical workflows to achieve novel results.
Guiding mathematical intuition with AI
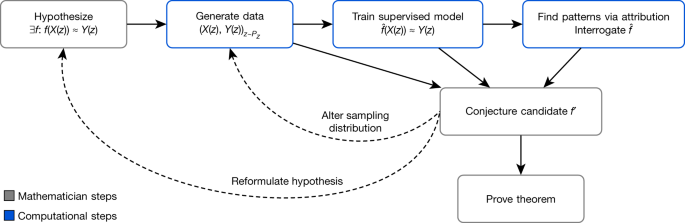
A mathematician’s intuition plays an enormously important role in mathematical discovery—“It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems”25. The following framework, illustrated in Fig. 1, describes a general method by which mathematicians can use tools from machine learning to guide their intuitions concerning complex mathematical objects, verifying their hypotheses about the existence of relationships and helping them understand those relationships. We propose that this is a natural and empirically productive way that these well-understood techniques in statistics and machine learning can be used as part of a mathematician’s work.
The process helps guide a mathematician’s intuition about a hypothesized function f, by training a machine learning model to estimate that function over a particular distribution of data PZ. The insights from the accuracy of the learned function and attribution techniques applied to it can aid in the understanding of the problem and the construction of a closed-form f′. The process is iterative and interactive, rather than a single series of steps.
Concretely, it helps guide a mathematician’s intuition about the relationship between two mathematical objects X(z) and Y(z) associated with z by identifying a function such that (X(z)) ≈ Y(z) and analysing it to allow the mathematician to understand properties of the relationship. As an illustrative example: let z be convex polyhedra, X(z) ∈ be the number of vertices and edges of z, as well as the volume and surface area, and Y(z) ∈ ℤ be the number of faces of z. Euler’s formula states that there is an exact relationship between X(z) and Y(z) in this case: X(z) · (−1, 1, 0, 0) + 2 = Y(z). In this simple example, among many other ways, the relationship could be rediscovered by the traditional methods of data-driven conjecture generation1. However, for X(z) and Y(z) in higher-dimensional spaces, or of more complex types, such as graphs, and for more complicated, nonlinear , this approach is either less useful or entirely infeasible.
The framework helps guide the intuition of mathematicians in two ways: by verifying the hypothesized existence of structure/patterns in mathematical objects through the use of supervised machine learning; and by helping in the understanding of these patterns through the use of attribution techniques.
In the supervised learning stage, the mathematician proposes a hypothesis that there exists a relationship between X(z) and Y(z). By generating a dataset of X(z) and Y(z) pairs, we can use supervised learning to train a function that predicts Y(z), using only X(z) as input. The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned given a sufficient amount of data. If is more accurate than would be expected by chance, it indicates that there may be such a relationship to explore. If so, attribution techniques can help in the understanding of the learned function sufficiently for the mathematician to conjecture a candidate f′. Attribution techniques can be used to understand which aspects of are relevant for predictions of Y(z). For example, many attribution techniques aim to quantify which component of X(z) the function is sensitive to. The attribution technique we use in our work, gradient saliency, does this by calculating the derivative of outputs of , with respect to the inputs. This allows a mathematician to identify and prioritize aspects of the problem that are most likely to be relevant for the relationship. This iterative process might need to be repeated several times before a viable conjecture is settled on. In this process, the mathematician can guide the choice of conjectures to those that not just fit the data but also seem interesting, plausibly true and, ideally, suggestive of a proof strategy.
Conceptually, this framework provides a ‘test bed for intuition’—quickly verifying whether an intuition about the relationship between two quantities may be worth pursuing and, if so, guidance as to how they may be related. We have used the above framework to help mathematicians to obtain impactful mathematical results in two cases—discovering and proving one of the first relationships between algebraic and geometric invariants in knot theory and conjecturing a resolution to the combinatorial invariance conjecture for symmetric groups4, a well-known conjecture in representation theory. In each area, we demonstrate how the framework has successfully helped guide the mathematician to achieve the result. In each of these cases, the necessary models can be trained within several hours on a machine with a single graphics processing unit.
CONTINUE READING Advancing mathematics by guiding human intuition with AI | Nature
No comments:
Post a Comment