Friday, December 03, 2021

Maths researchers hail breakthrough in applications of artificial intelligence

For the first time, computer scientists and mathematicians have used artificial intelligence to help prove or suggest new mathematical theorems in the complex fields of knot theory and representation theory.

The astonishing results have been published today in the pre-eminent scientific journal, Nature.

Professor Geordie Williamson is Director of the University of Sydney Mathematical Research Institute and one of the world's foremost mathematicians. As a co-author of the paper, he applied the power of Deep Mind's AI processes to explore conjectures in his field of speciality, representation theory.

His co-authors were from DeepMind—the team of computer scientists behind AlphaGo, the first computer program to successfully defeat a world champion in the game of Go in 2016.

Professor Williamson said: "Problems in mathematics are widely regarded as some of the most intellectually challenging problems out there.

"While mathematicians have used machine learning to assist in the analysis of complex data sets, this is the first time we have used computers to help us formulate conjectures or suggest possible lines of attack for unproven ideas in mathematics."

Proving mathematical conjectures

Professor Williamson is a globally recognized leader in representation theory, the branch of mathematics that explores higher dimensional space using linear algebra.

In 2018 he was elected the youngest living Fellow of the Royal Society in London, the world's oldest and arguably most prestigious scientific association.

"Working to prove or disprove longstanding conjectures in my field involves the consideration of, at times, infinite space and hugely complex sets of equations across multiple dimensions," Professor Williamson said.

While computers have long been used to generate data for experimental mathematics, the task of identifying interesting patterns has relied mainly on the intuition of the mathematicians themselves.

That has now changed.

Professor Williamson used DeepMind's AI to bring him close to proving an old conjecture about Kazhdan-Lusztig polynomials, which has been unsolved for 40 years. The conjectures concern deep symmetry in higher dimensional algebra.

Co-authors Professor Marc Lackeby and Professor András Juhász from the University of Oxford have taken the process a step further. They discovered a surprising connection between algebraic and geometric invariants of knots, establishing a completely new theorem in mathematics.

In knot theory, invariants are used to address the problem of distinguishing knots from each other. They also help mathematicians understand properties of knots and how this relates to other branches of mathematics.

While of profound interest in its own right, knot theory also has myriad applications in the physical sciences, from understanding DNA strands, fluid dynamics and the interplay of forces in the Sun's corona.

Professor Juhász said: "Pure mathematicians work by formulating conjectures and proving these, resulting in theorems. But where do the conjectures come from?

"We have demonstrated that, when guided by mathematical intuition, machine learning provides a powerful framework that can uncover interesting and provable conjectures in areas where a large amount of data is available, or where the objects are too large to study with classical methods."

Professor Lackeby said: "It has been fascinating to use machine learning to discover new and unexpected connections between different areas of mathematics. I believe that the work that we have done in Oxford and in Sydney in collaboration with DeepMind demonstrates that machine learning can be a genuinely useful tool in mathematical research."

Lead author from DeepMind, Dr. Alex Davies, said: "We think AI techniques are already sufficiently advanced to have an impact in accelerating scientific progress across many different disciplines. Pure maths is one example and we hope that this Nature paper can inspire other researchers to consider the potential for AI as a useful tool in the field."

Professor Williamson said: "AI is an extraordinary tool. This work is one of the first times it has demonstrated its usefulness for pure mathematicians, like me."

"Intuition can take us a long way, but AI can help us find connections the human mind might not always easily spot."

The authors hope that this work can serve as a model for deepening collaboration between fields of mathematics and artificial intelligence to achieve surprising results, leveraging the respective strengths of mathematics and machine learning.

"For me these findings remind us that intelligence is not a single variable, like an IQ number. Intelligence is best thought of as a multi-dimensional space with multiple axes: academic intelligence, emotional intelligence, social intelligence," Professor Williamson said.

"My hope is that AI can provide another axis of intelligence for us to work with, and that this new axis will deepen our understanding of the mathematical world."

The Ramanujan Machine: Researchers have developed a 'conjecture generator' that creates mathematical conjectures

More information: Alex Davies, Advancing mathematics by guiding human intuition with AI, Nature (2021). DOI: 10.1038/s41586-021-04086-x. www.nature.com/articles/s41586-021-04086-x

Journal information: Nature

Provided by University of Sydney

Mathematical discoveries take intuition and creativity – and now a little help from AI

December 1, 2021 12.10pm EST

Research in mathematics is a deeply imaginative and intuitive process. This might come as a surprise for those who are still recovering from high-school algebra.

What does the world look like at the quantum scale? What shape would our universe take if we were as large as a galaxy? What would it be like to live in six or even 60 dimensions? These are the problems that mathematicians and physicists are grappling with every day.

To find the answers, mathematicians like me try to find patterns that relate complicated mathematical objects by making conjectures (ideas about how those patterns might work), which are promoted to theorems if we can prove they are true. This process relies on our intuition as much as our knowledge.

Over the past few years I’ve been working with experts at artificial intelligence (AI) company DeepMind to find out whether their programs can help with the creative or intuitive aspects of mathematical research. In a new paper published in Nature, we show they can: recent techniques in AI have been essential to the discovery of a new conjecture and a new theorem in two fields called “knot theory” and “representation theory”.

Get your news from people who know what they’re talking about.Sign up for newsletter
Machine intuition

Where does the intuition of a mathematician come from? One can ask the same question in any field of human endeavour. How does a chess grandmaster know their opponent is in trouble? How does a surfer know where to wait for a wave?

The short answer is we don’t know. Something miraculous seems to happen in the human brain. Moreover, this “miraculous something” takes thousands of hours to develop and is not easily taught

.
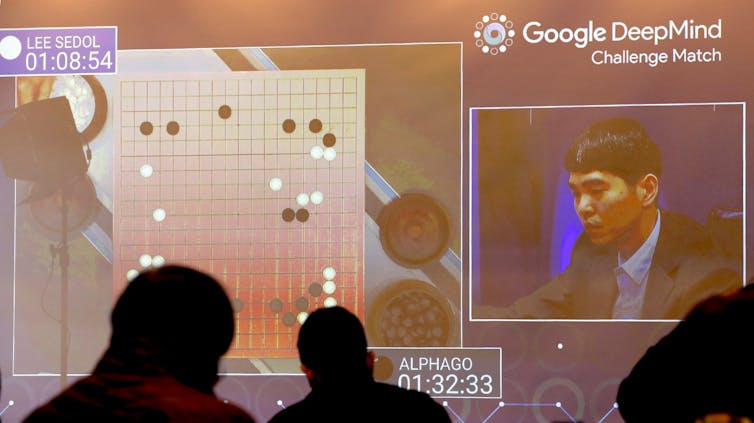
The AlphaGo software’s defeat of Lee Sedol in 2016 is regarded as one of the most striking early examples of a machine displaying something like human intuition.

Lee Jin-man / AP

The past decade has seen computers display the first hints of something like human intuition. The most striking example of this occurred in 2016, in a Go match between DeepMind’s AlphaGo program and Lee Sedol, one of the world’s best players.

AlphaGo won 4–1, and experts observed that some of AlphaGo’s moves displayed human-level intuition. One particular move (“move 37”) is now famous as a new discovery in the game.

Read more: AI has beaten us at Go. So what next for humanity?

How do computers learn?

Behind these breakthroughs lies a technique called deep learning. On a computer one builds a neural network – essentially a crude mathematical model of a brain, with many interconnected neurons.

At first, the network’s output is useless. But over time (from hours to even weeks or months), the network is trained, essentially by adjusting the firing rates of the neurons.

Such ideas were tried in the 1970s with unconvincing results. Around 2010, however, a revolution occurred when researchers drastically increased the number of neurons in the model (from hundreds in the 1970s to billions today).

One of the first neural networks, the Mark I Perceptron, was built in the 1950s. The goal was to classify digital images, but results were disappointing. Cornell University

Traditional computer programs struggle with many tasks humans find easy, such as natural language processing (reading and interpreting text), and speech and image recognition.

With the deep learning revolution of the 2010s, computers began performing well on these tasks. AI has essentially brought vision and speech to machines.

Training neural nets requires huge amounts of data. What’s more, trained deep learning models often function as “black boxes”. We know they often give the right answer, but we usually don’t know (and can’t ascertain) why.

Deep learning systems often function as ‘black boxes’: data goes in and data comes out, but we have difficulty making sense of what happens in between. Shutterstock

A lucky encounter

My involvement with AI began in 2018, when I was elected a Fellow of the Royal Society. At the induction ceremony in London I met Demis Hassabis, chief executive of DeepMind.

Over a coffee break we discussed deep learning, and possible applications in mathematics. Could machine learning lead to discoveries in mathematics, like it had in Go?

This fortuitous conversation led to my collaboration with the team at DeepMind.

A meeting with AI pioneer Demis Hassabis led to the current work on creative uses of machine learning in mathematical research. Wu Hong / EPA

Mathematicians like myself often use computers to check or perform long computations. However, computers usually cannot help me develop intuition or suggest a possible line of attack. So we asked ourselves: can deep learning help mathematicians build intuition?

With the team from DeepMind, we trained models to predict certain quantities called Kazhdan-Lusztig polynomials, which I have spent most of my mathematical life studying.

In my field we study representations, which you can think of as being like molecules in chemistry. In much the same way that molecules are made of atoms, the make up of representations is governed by Kazhdan-Lusztig polynomials.

Amazingly, the computer was able to predict these Kazhdan-Lusztig polynomials with incredible accuracy. The model seemed to be onto something, but we couldn’t tell what.

However, by “peeking under the hood” of the model, we were able to find a clue which led us to a new conjecture: that Kazhdan-Lusztig polynomials can be distilled from a much simpler object (a mathematical graph).

This conjecture suggests a way forward on a problem that has stumped mathematicians for more than 40 years. Remarkably, for me, the model was providing intuition!

Read more: How explainable artificial intelligence can help humans innovate

In parallel work with DeepMind, mathematicians Andras Juhasz and Marc Lackenby at the University of Oxford used similar techniques to discover a new theorem in the mathematical field of knot theory. The theorem gives a relation between traits (or “invariants”) of knots that arise from different areas of the mathematical universe.

Our paper reminds us that intelligence is not a single variable, like the result of an IQ test. Intelligence is best thought of as having many dimensions.

My hope is that AI can provide another dimension, deepening our understanding of the mathematical world, as well as the world in which we live.

Author

Geordie Williamson
Professor of Mathematics, University of Sydney
Disclosure statement
Geordie Williamson is a Professor at the University of Sydney, and a consultant in Pure Mathematics for DeepMind, a subsidiary of Alphabet.

Advancing mathematics by guiding human intuition with AI

Alex Davies,

Demis Hassabis &

Nature volume 600, pages70–74 (2021)Cite this article

Metricsdetails

Abstract

The practice of mathematics involves discovering patterns and using these to formulate and prove conjectures, resulting in theorems. Since the 1960s, mathematicians have used computers to assist in the discovery of patterns and formulation of conjectures1, most famously in the Birch and Swinnerton-Dyer conjecture2, a Millennium Prize Problem3. Here we provide examples of new fundamental results in pure mathematics that have been discovered with the assistance of machine learning—demonstrating a method by which machine learning can aid mathematicians in discovering new conjectures and theorems. We propose a process of using machine learning to discover potential patterns and relations between mathematical objects, understanding them with attribution techniques and using these observations to guide intuition and propose conjectures. We outline this machine-learning-guided framework and demonstrate its successful application to current research questions in distinct areas of pure mathematics, in each case showing how it led to meaningful mathematical contributions on important open problems: a new connection between the algebraic and geometric structure of knots, and a candidate algorithm predicted by the combinatorial invariance conjecture for symmetric groups4. Our work may serve as a model for collaboration between the fields of mathematics and artificial intelligence (AI) that can achieve surprising results by leveraging the respective strengths of mathematicians and machine learning.

Main

One of the central drivers of mathematical progress is the discovery of patterns and formulation of useful conjectures: statements that are suspected to be true but have not been proven to hold in all cases. Mathematicians have always used data to help in this process—from the early hand-calculated prime tables used by Gauss and others that led to the prime number theorem5, to modern computer-generated data1,5 in cases such as the Birch and Swinnerton-Dyer conjecture2. The introduction of computers to generate data and test conjectures afforded mathematicians a new understanding of problems that were previously inaccessible6, but while computational techniques have become consistently useful in other parts of the mathematical process7,8, artificial intelligence (AI) systems have not yet established a similar place. Prior systems for generating conjectures have either contributed genuinely useful research conjectures9 via methods that do not easily generalize to other mathematical areas10, or have demonstrated novel, general methods for finding conjectures11 that have not yet yielded mathematically valuable results.

AI, in particular the field of machine learning12,13,14, offers a collection of techniques that can effectively detect patterns in data and has increasingly demonstrated utility in scientific disciplines15. In mathematics, it has been shown that AI can be used as a valuable tool by finding counterexamples to existing conjectures16, accelerating calculations17, generating symbolic solutions18 and detecting the existence of structure in mathematical objects19. In this work, we demonstrate that AI can also be used to assist in the discovery of theorems and conjectures at the forefront of mathematical research. This extends work using supervised learning to find patterns20,21,22,23,24 by focusing on enabling mathematicians to understand the learned functions and derive useful mathematical insight. We propose a framework for augmenting the standard mathematician’s toolkit with powerful pattern recognition and interpretation methods from machine learning and demonstrate its value and generality by showing how it led us to two fundamental new discoveries, one in topology and another in representation theory. Our contribution shows how mature machine learning methodologies can be adapted and integrated into existing mathematical workflows to achieve novel results.

Guiding mathematical intuition with AI

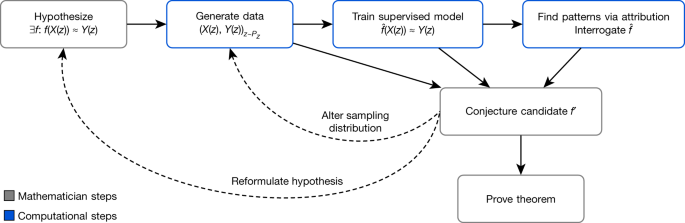
A mathematician’s intuition plays an enormously important role in mathematical discovery—“It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems”25. The following framework, illustrated in Fig. 1, describes a general method by which mathematicians can use tools from machine learning to guide their intuitions concerning complex mathematical objects, verifying their hypotheses about the existence of relationships and helping them understand those relationships. We propose that this is a natural and empirically productive way that these well-understood techniques in statistics and machine learning can be used as part of a mathematician’s work.

Concretely, it helps guide a mathematician’s intuition about the relationship between two mathematical objects X(z) and Y(z) associated with z by identifying a function $\hat{f}$ such that $\hat{f}$ (X(z)) ≈ Y(z) and analysing it to allow the mathematician to understand properties of the relationship. As an illustrative example: let z be convex polyhedra, X(z) ∈ $Z^{2} \times R^{2}$ be the number of vertices and edges of z, as well as the volume and surface area, and Y(z) ∈ ℤ be the number of faces of z. Euler’s formula states that there is an exact relationship between X(z) and Y(z) in this case: X(z) · (−1, 1, 0, 0) + 2 = Y(z). In this simple example, among many other ways, the relationship could be rediscovered by the traditional methods of data-driven conjecture generation1. However, for X(z) and Y(z) in higher-dimensional spaces, or of more complex types, such as graphs, and for more complicated, nonlinear $\hat{f}$ , this approach is either less useful or entirely infeasible.

The framework helps guide the intuition of mathematicians in two ways: by verifying the hypothesized existence of structure/patterns in mathematical objects through the use of supervised machine learning; and by helping in the understanding of these patterns through the use of attribution techniques.

In the supervised learning stage, the mathematician proposes a hypothesis that there exists a relationship between X(z) and Y(z). By generating a dataset of X(z) and Y(z) pairs, we can use supervised learning to train a function $\hat{f}$ that predicts Y(z), using only X(z) as input. The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned given a sufficient amount of data. If $\hat{f}$ is more accurate than would be expected by chance, it indicates that there may be such a relationship to explore. If so, attribution techniques can help in the understanding of the learned function $\hat{f}$ sufficiently for the mathematician to conjecture a candidate f′. Attribution techniques can be used to understand which aspects of $\hat{f}$ are relevant for predictions of Y(z). For example, many attribution techniques aim to quantify which component of X(z) the function $\hat{f}$ is sensitive to. The attribution technique we use in our work, gradient saliency, does this by calculating the derivative of outputs of $\hat{f}$ , with respect to the inputs. This allows a mathematician to identify and prioritize aspects of the problem that are most likely to be relevant for the relationship. This iterative process might need to be repeated several times before a viable conjecture is settled on. In this process, the mathematician can guide the choice of conjectures to those that not just fit the data but also seem interesting, plausibly true and, ideally, suggestive of a proof strategy.

Conceptually, this framework provides a ‘test bed for intuition’—quickly verifying whether an intuition about the relationship between two quantities may be worth pursuing and, if so, guidance as to how they may be related. We have used the above framework to help mathematicians to obtain impactful mathematical results in two cases—discovering and proving one of the first relationships between algebraic and geometric invariants in knot theory and conjecturing a resolution to the combinatorial invariance conjecture for symmetric groups4, a well-known conjecture in representation theory. In each area, we demonstrate how the framework has successfully helped guide the mathematician to achieve the result. In each of these cases, the necessary models can be trained within several hours on a machine with a single graphics processing unit.

CONTINUE READING Advancing mathematics by guiding human intuition with AI | Nature

Astrocolonialism: Big tech is stealing the night sky from humans

Twinkle twinkle little light, now I wonder whether you're a star or a satellite

STORY BY
Tristan Greene

Everybody deserves to have internet access. It’s as crucial to our ability to thrive in modern society as running water and electricity.

Getting that access to rural and/or impoverished areas is one of the great technology challenges of our time. Unfortunately, the people who’ve stepped up the most are those hoping to profit from humanity’s problems at any cost.

To that end, companies such as SpaceX, Amazon, OneWeb, and StarNet/GW have decided it’s in their financial best interest to capitalize on the problem by littering the Earth’s orbit with tens of thousands of satellites meant to provide internet services to those who, otherwise, might not have access.

Currently more than half of all operational satellites orbiting the Earth are SpaceX satellites. The vast majority of which were designed and launched with little or no consideration concerning how reflective they are.

What does that mean, scientifically speaking? It means in the near future there will be no place on Earth from which any living being can gaze upon the naked night sky again. Ever.

According to simulations from a team of Canadian astrophysicists (who specialize in research that’s currently being harmed by light pollution from big tech’s satellites), a whopping one in fifteen sources of light we see in the night sky will soon be artificial.

Whether you’re standing at the North Pole, the South Pole, the equator, or anywhere in-between: the 65,000+ satellites that big tech companies plan to litter the sky with will ensure you never see the night sky again as your grandparents did.

And, sadly, there’s no turning back. According to the Canadian research team, even if SpaceX and other companies continue to focus on designing less-reflective satellites, our view of the night sky is essentially changed forever.

Per the team’s paper:

The simulations presented here show how the effects of satcons are a long-term change to the night sky worldwide, which is a shared resource enjoyed and used by humanity.

There is simply no way to have tens of thousands of satellites in Low Earth Orbit and avoid consequences for astronomy.

But with strong, international cooperation and appropriate regulation of satellite numbers, reflectivities, and satellite broadcasting, we can perhaps reach a compromise that allows much of research astronomy and traditional naked-eye stargazing to continue with minor losses.

Unfortunately, any expectations of “strong, international cooperation” and “appropriate regulation of satellite numbers” is pie-in-the-sky fantasy.

We may as well ask the US and Chinese governments to set their differences aside and become a single nation together. There’s a better chance of that happening than Elon Musk or Jeff Bezos deciding to regulate their own multi-billion (trillion! in the case of Bezos) dollar enterprises for the good of humanity.

The simple fact of the matter is there’s next to no regulations concerning civilian enterprises in Earth’s orbit. If SpaceX and Amazon want to fill the night sky so completely that we can’t squeeze a glance at a real star through the light pollution, there’s not much to stop them – something that’s evident by the fact that tens of thousands of more satellites are scheduled to enter the skies over the course of the next handful of years.

Worse, most of these satellites will only have a short lifespan. That means they’ll be regularly deorbited and replaced – and by “deorbited” we mean moved out of the way and left in the Earth’s upper atmosphere where they’ll become highly-reflective space trash.

Per an article on Phys.Org by the paper’s lead author, astrophysicist Samantha Lawler:

Starlink plans to replace each of the 42,000 satellites [that it’s planning to launch] after five years of operation, which will require de-orbiting an average 25 satellites per day, about six tons of material.

The mass of these satellites won’t go away—it will be deposited in the upper atmosphere. Because satellites comprise mostly aluminum alloys, they may form alumina particles as they vaporize in the upper atmosphere, potentially destroying ozone and causing global temperature changes.

This has not yet been studied in-depth because low Earth orbit is not currently subject to any environmental regulations.

So let’s summarize:
If you’re over the age of four-years-old, you can no longer see the night sky as it looked when you were born.
Within a matter of years, approximately one in every 15 sources of light in the night sky visible to the naked eye from Earth will be artificial.
Whether you use satellite internet from SpaceX or Amazon is irrelevant. There’s no regulation stopping big tech from astrocolonization – taking something that belongs to everyone and claiming it for themselves. You don’t get a vote in whether you get to see the stars or not.

On the bright side, however: Elon Musk and Jeff Bezos are the richest people who have ever lived. You get to be a part of that. Our collective willingness to let these men destroy our natural resources is their greatest business asset.

I can’t wait to see what else we’ll lose, as a species, in service of Elon and Jeff’s fortunes.

This amazing new physics theory made me believe time travel is possible

By any chance, do you happen to know where the information goes?

STORY BY
Tristan Greene

There’s a lot of discussion about “time” in the world of quantum physics. At the micro level, where waves and particles can behave the same, time tends to be much more malleable than it is in our observable realm of classical physics.

Think about the clock on the wall. You can push the hands backwards, but that doesn’t cause time itself to rewind. Time marches on.

But things are much simpler in the quantum realm. If we can mathematically express particulate activity in one direction, then we can mathematically express it in a diametric one.

In other words: time travel actually makes sense through a quantum lens. Whatever goes forward must be able to go backward.

Related: Google’s ‘time crystals’ could be the greatest scientific achievement of our lifetimes

But it all falls apart when we get back to classical physics. I don’t care how much math you do, you can’t unbreak a bottle, untell a secret, or unshoot a gun.

As Gid’on Lev points out in a recent article on Haaretz, this disparity between quantum and classical physics is one of the field’s biggest challenges.

Per Lev’s article:

Hawking demonstrated that regarding black holes, one of the two major theories leads to an error.

According to his calculations, the radiation emitted by the hole is not a function of the material the hole swallows, and therefore, two black holes that formed by different processes will emit the same exact radiation. This meant that the information on every physical particle swallowed into the black hole, including its mass, speed of movement, etc., disappears from the universe.

But under the theory of quantum mechanics, such deletion is impossible.
Hawking was wrong, then he was right

Lev’s article goes on to explain how Stephen Hawking eventually conceded (he lost a bet) that the information entering a black hole wasn’t gone. He, of course, couldn’t explain exactly where it went. But most physicists were pretty sure it had to go somewhere – nothing else in the universe just vanishes.

Fast forward to 2019 and two separate research teams (working independently of each other) published pre-print papers seemingly confirming Hawking’s hunch about the persistence of information.

Not only were the papers published within 24 hours of each other, but the lead authors on each ended up sharing the 2021 New Horizons Breakthrough Prize for Fundamental Physics.

What both teams discovered was that a slight change in perspective made all the math line up.

When information enters a black hole it appears to be lost because, for all intents and purposes, it’s no longer available to the universe.

And that’s what stumped Hawking. Imagine a single photon of light getting caught in a black hole and swallowed up. Hawking and his colleagues knew the photon (and the information that was swallowed up with it) couldn’t be deleted.

But, according to Hawking, black holes leak thermal radiation. And that means they eventually lose their energy and mass and… fade away.

Hawking and company couldn’t figure out how to reconcile the fact that once a black hole is gone, anything that’s ever been inside it appears to be gone too.

That’s because they were looking in the wrong places. Hawking and others were trying to find signs of the missing information leaking out simiarly along a black hole’s event horizon.

Unfortunately, using the event horizon as a starting point never panned out – the numbers didn’t quite add up.

The 2021 New Horizons Prize winners figured out a different way to measure the “area” of a black hole. And, by applying the new lens to measurements over various stages of a black hole’s life, they were finally able to make the numbers add up.
Here’s how this relates to time travel

If these two teams did in fact demonstrate that even a black hole can’t render information irreversible, then there might be nothing physically stopping us from time travel.

And I’m not talking about that hard-to-explain, gravity at the edge of a black hole, your friends would get older while you stayed young kind of time travel.

I’m talking about real-life Marty Mcfly time travel where you could set the dials in the DeLorean for 13 March 1986 so you could go back and invest in Microsoft on the day its stock went public.

Now, much like Stephen Hawking, I don’t have any math or engineering solutions to the problem at hand. I’ve just got this physics theory.

If information can and does escape from black holes, then it’s only logical to assume that other processes which we only see in quantum mechanics could also be explained through classical physics.

We know that time travel is possible in quantum mechanics. Google demonstrated this by building time crystals, and numerous quantum computing paradigms rely on a form of prediction that surfaces answers using what’s basically molecular time-travel.

But we all know that, when it comes to quantum stuff, we’re talking about particles demonstrating counter-intuitive behavior. That’s not the same thing as pushing a button and making a car from the 1980s appear back in the old Wild West.

However, that doesn’t mean quantum time travel isn’t just as mind-blowing. Translating time crystals into something analogous in classical physics would mean creating donuts that reappear on your plate after you eat them or beer that reappears in your glass no matter how many times you chug it.

If we concede that time crystals exist and information can escape a black hole, then we have to admit that donuts – or anything, even people – could one day travel through time too.

Then again, nobody showed up for Hawking’s party. So, either it isn’t possible or time travelers are jerks.

Misinformation fuelled by ‘tsunami’ of poor research, says science prize winner

Dutch microbiologist Elisabeth Bik, winner of prestigious John Maddox prize, says trust in science is being undermined

Elisabeth Bik won the John Maddox prize for standing up for science in the face of harassment, intimidation and lawsuits.

Photograph: Amy Osborne/AFP/Getty Images

Hannah Devlin Science correspondent
THE GUARDIAN
Wed 1 Dec 2021

A “tsunami” of poor quality research is fuelling misinformation and could undermine trust in science, the winner of the prestigious John Maddox prize has warned.

Elisabeth Bik, a Dutch microbiologist turned science sleuth who on Wednesday evening won the John Maddox prize for standing up for science in the face of harassment, intimidation and lawsuits, said the intense pressure to publish papers is leading to a “dilution” of the quality of scientific literature.

This risks flawed work being “amplified by bad actors” such as those seeking to stoke fears about vaccination.

“The danger with social media is that even a mediocre or bad or flawed paper can be taken by people who have different agendas and brought into the spotlight and celebrated as the new truth,” Bik said. “That is a new danger that has not been there before.”

She cited a recently retracted paper linking the HPV vaccine to female infertility and another that appeared to overstate the risk of myocarditis from Covid vaccines.

Bik has been recognised for her work exposing problems including image doctoring, plagiarism, data manipulation and unsound methodology.

She took up the campaign after discovering her own work had been plagiarised in 2013, and in 2019 left her job at a biotech firm to pursue the issue full time, funding her work through a Patreon account.

After raising serious concerns about claims that hydroxychloroquine was effective in treating Covid infections, Bik faced online harassment and threats of violence. Larger trials found no evidence to support the use of hydroxychloroquine to treat Covid patients.

The controversial French professor behind the work, Didier Raoult, threatened legal action against her, which she described as “scary and intimidating”.

In general, Bik said, the intense demand for solutions to the global pandemic has created a new pressure for scientists to deliver breakthroughs.

“A lot of scientists wanted to become the big saviour of the pandemic,” she said. “That brought a lot of fraud or just even poorly executed research. People want to become a hero and might go to great lengths to achieve that.”

This vision of the heroic scientist sits in contrast to the reality of life in the laboratory, Bik said. “Ninety percent of your results will be failures, every now and again you’ll get a success … but most of the time it’s sad and boring to be in the lab,” she said. “You can work really hard in science and still not get the results everyone hoped for. You have to be able to deal with that.”

Through her Science Integrity Digest, Bik encourages the public and other scientists to learn how to spot manipulated data. Her work has led to the retraction of around 600 papers and she derives “some satisfaction” from setting the record straight. But she has a spreadsheet of nearly 5,000 papers that she has reported as problematic and says the overall response from scientific publishers has been disappointing.

“We [scientists] write the papers for free, we peer review them for free and then still we have to pay the publisher $4,000 to get our paper published,” she said. “Where does that money go to? It seems a lot of people sitting in shiny offices, bosses of bosses of bosses, people who don’t seem to be doing something directly to my paper. It’s hard to justify.”

Bik said that winning the prize was a “great honour and delight”. The prizes are awarded jointly by the charity Sense about Science and the journal Nature, where John Maddox was a former editor.

Tracey Brown, the director of Sense about Science, said: “The shocking thing about what Elisabeth is doing in challenging fraud and misrepresentation of scientific findings is that this is something that most people think already happens. Only it doesn’t. And in fact she has been unique and often alone in sounding the alarm. The judges were struck by her unstinting determination.”

A second John Maddox prize for an early career researcher was awarded to Mohammad Sharif Razai, a GP and researcher at St George’s, University of London, for bringing an evidence-based understanding of racial health inequalities to bear in public and policy debates. Razai’s work has covered vaccine hesitancy among ethnic minority groups and systemic racism as a cause of adverse health outcomes.

When variations in Earth's orbit drive biological evolution

by CNRS

Coccolithophores are microscopic algae that form tiny limestone plates, called coccoliths, around their single cells. The shape and size of coccoliths varies according to the species. After their death, coccolithophores sink to the bottom of the ocean and their coccoliths accumulate in sediments, which faithfully record the detailed evolution of these organisms over geological time.

A team of scientists led by CNRS researchers show, in an article published in Nature on December 1, 2021, that certain variations in Earth's orbit have influenced the evolution of coccolithophores. To achieve this, no less that 9 million coccoliths, spanning an interval of 2.8 million years and several locations in the tropical ocean, were measured and classified using automated microscope techniques and artificial intelligence.

The researchers observed that coccoliths underwent cycles of higher and lower diversity in size and shape, with rhythms of 100 and 400 thousand years. They also propose a cause: the more or less circular shape of Earth's orbit around the Sun, which varies at the same rhythms. Thus, when Earth's orbit is more circular, as is the case today (this is known as low eccentricity), the equatorial regions show little seasonal variation and species that are not very specialized dominate all the oceans. Conversely, as eccentricity increases and more pronounced seasons appear near the equator, coccolithophores diversify into many specialized species, but collectively produce less limestone.

Crucially, due to their abundance and global distribution, these organisms are responsible for half of the limestone (calcium carbonate, partly composed of carbon) produced in the oceans and therefore play a major role in the carbon cycle and in determining ocean chemistry. It is therefore likely that the cyclic abundance patterns of these limestone producers played a key role in ancient climates, and may explain hitherto mysterious climate variations in past warm periods.

In other words, in the absence of ice, the biological evolution of micro-algae could have set the tempo of climates. This hypothesis remains to be confirmed.The smallest skeletons in the marine world observed in 3-D by synchrotron techniquesMore information: Luc Beaufort, Cyclic evolution of phytoplankton forced by changes in tropical seasonality, Nature (2021). DOI: 10.1038/s41586-021-04195-7. www.nature.com/articles/s41586-021-04195-7

Journal information: Nature

Provided by CNRS

Research aircraft reveal a surprisingly strong Southern Ocean carbon sink

by National Center for Atmospheric Research

The Southern Ocean is a significant carbon sink, absorbing a large amount of the excess carbon dioxide emitted into the atmosphere by human activities, according to a new study led by the National Center for Atmospheric Research (NCAR).

The findings provide clarity about the role the icy waters surrounding Antarctica play in buffering the impact of increasing greenhouse gas emissions, after research published in recent years suggested the Southern Ocean might be less of a sink than previously thought.

The new study, published this week in the journal Science, makes use of observations from research aircraft flown during three field projects over nearly a decade, as well as a collection of atmospheric models, to determine that the Southern Ocean takes up significantly more carbon than it releases. The research also highlights the power that airborne observations have to reveal critical patterns in the global carbon cycle.

"You can't fool the atmosphere," said NCAR scientist Matthew Long, the paper's lead author. "While measurements taken from the ocean surface and from land are important, they are too sparse to provide a reliable picture of air-sea carbon flux. The atmosphere, however, can integrate fluxes over large expanses. Airborne measurements show a drawdown of CO2 in the lower atmosphere over the Southern Ocean surface in summer, indicating carbon uptake by the ocean."

Uncertainty about the role of the Southern Ocean

Once human-produced emissions of CO2—from burning fossil fuels and other activities—enter the atmosphere, some of the gas is taken up by plants and some is absorbed into the ocean. While the overall concentration of CO2 in the atmosphere continues to increase, causing the global temperature to rise, these land and ocean "sinks" slow the effect.

A more precise understanding of where carbon sinks exist, how big they are, and how they may be changing as society continues to emit more CO2 is crucial to projecting the future trajectory of climate change. It is also necessary for evaluating the impact of potential emission reduction measures and CO2 removal technologies.

Scientists have long thought that the Southern Ocean is an important carbon sink. In the region around Antarctica, cold water from the deep ocean is transported to the surface. This upwelling water may not have seen the surface of the ocean for hundreds of years—but once in contact with the atmosphere, it's able to absorb CO2 before sinking again.

Measurements of CO2 and related properties in the ocean suggest that 40 percent of all human-produced CO2 now stored in the ocean was originally taken up by the Southern Ocean. But measuring the actual flux at the surface—the back and forth exchange of CO2 between the water and the overlying air throughout a year—has been challenging.

In recent years, scientists have used observations of pH taken from autonomous floats deployed in the Southern Ocean to infer information about air-sea carbon flux. The results of those efforts suggested that the carbon sink in the Southern Ocean might be much smaller than previously thought. The possibility that the prevailing understanding of the role the Southern Ocean plays in the carbon cycle might be wrong generated a lot of discussion within the scientific community and left unanswered questions, including where the excess CO2 is going if not into the Southern Ocean. Could there be a significant sink on land or elsewhere in the global oceans that scientists have missed?

The DC-8 flying laboratory on ATom's second deployment carried over 30 instruments to sample the atmosphere. Credit: Chelsea Thompson, NOAA

The value of atmospheric measurements

In the new study, the research team sought to address the uncertainty by looking at carbon in the air instead of in the water. The atmosphere and the ocean exist in balance, and they are constantly exchanging CO2, oxygen, and other gases with each other.

The research team pieced together airborne measurements from three different field projects with deployments stretching over nearly a decade: the HIAPER Pole-to-Pole Observations (HIPPO) project, the O2/N2 Ratio and CO2 Airborne Southern Ocean (ORCAS) study, and the Atmospheric Tomography (ATom) mission.

While there are also surface monitoring stations that measure CO2 in the atmosphere over the Southern Ocean, these stations are relatively few and far between, making it difficult to characterize what is happening across the entire region.

"The atmospheric CO2 signals over the Southern Ocean are small and challenging to measure, especially from surface stations using different instruments run by different laboratories," said NCAR scientist Britton Stephens, a co-author of the study who co-led or participated in all of the field campaigns. "But with the suite of high-performance instrumentation we flew, the signals were striking and unequivocal."

Critically, the data from the aircraft campaigns captured the vertical CO2 gradient. For example, during the NSF-funded ORCAS field campaign, which took place in January and February 2016, Stephens, Long, and other scientists on board the NSF/NCAR HIAPER Gulfstream V research aircraft could see a decrease in CO2 concentrations on their instruments as the plane descended.

"Every time the GV dipped near the surface, turbulence increased—indicating the air was in contact with the ocean—at precisely the moment when all the CO2 instruments registered a drop in concentrations," Stephens said. "You could feel it."

The new study finds that this gradient is quite sensitive to the air-sea carbon flux, offering researchers an unprecedented opportunity to characterize the Southern Ocean's carbon uptake.

"We needed observations that included both intensive surveys at a particular time of the year and that spanned the seasonal cycle," Long said. "That was the motivation for combining multiple aircraft campaigns that span roughly a decade. We were able to aggregate them together to assess the mean seasonal cycle of CO2 variability in the atmosphere."

After piecing together how CO2 typically varies in the atmosphere at a particular time of the year, the research team turned to a suite of atmospheric models to help them translate their atmospheric profiles into an estimate of how much CO2 the ocean was soaking up or releasing. Their conclusion was that the Southern Ocean takes in significantly more carbon in the summer than it loses during the winter, absorbing a whopping 2 billion tons of CO2 over the course of a year. In the summer, blooms of photosynthetic algae, or phytoplankton, play a key role in driving CO2 uptake into the ocean.

The research team noted that a regular program of future airborne observations over the Southern Ocean could also help scientists understand whether the area's capacity to continue taking up carbon may change in the future. A similar measurement strategy could yield important information in other regions of the globe too.

"We've really seen that these observations are hugely powerful," Long said. "Future aircraft observations could yield extremely high scientific value for the investment. It's critical that we have a finger on the pulse of the carbon cycle as we enter a period when global society is taking action to reduce CO2 in the atmosphere. These observations can help us do just that."Uncertainty of future Southern Ocean carbon dioxide uptake cut in half

More information: Matthew Long, Strong Southern Ocean Carbon Uptake Evident in Airborne Observations, Science (2021). DOI: 10.1126/science.abi4355. www.science.org/doi/10.1126/science.abi4355

Journal information: Science

Provided by National Center for Atmospheric Research

Zapping cow dung with lightning is helping to trap climate-warming methane

Story by Reuters
Wed December 1, 2021

Dairy cows at a test farm in Buckinghamshire, England, where the Oslo-based company N2 Applied is testing plasma technology to prevent methane emissions.

A Norwegian technology company has found a way to stop livestock slurry from releasing methane -- by zapping it with artificial lightning.

Methane is a potent greenhouse gas emitted from sources including leaky fossil fuel infrastructure, landfill sites and livestock farming.

Oslo-based N2 Applied is testing its plasma technology at several sites in Europe, including on three farms in the UK.

"In essence, we're harnessing lightning to zap livestock slurry and lock in harmful emissions," N2's Chris Puttick told Reuters at one of the test farms in Buckinghamshire, England.

At this site, 200 dairy cows are providing the raw material: dung.
A manure scrapper collects all the excrement from the barn floor and deposits it in a pit where it is then moved through the N2 machine, housed in a standard-sized shipping container. Nitrogen from the air and a blast from a 50 kilowatt plasma torch is forced through the slurry 'locking in' both methane and ammonia emissions.

Scientists say this invisible gas could seal our fate on climate change

"When we add nitrogen from air to the slurry, it changes the environment to stop methanogenesis basically. So it drops the pH down to just below six and we're catching that early. So it stops the breakdown of those methane microbes that then release the gas to the air," Puttick said, adding their patented technology is the only one of its kind.
What comes out of the machine is an odorless brown liquid, called NEO -- a Nitrogen Enriched Organic fertilizer.
According to N2, their NEO has double the nitrogen content of regular nitrogen fertilizer; one of the most commonly used fertilizers to boost production of corn, canola and other crops.
Puttick said independent tests showed their technology reduces methane emissions from slurry by 99%. It also cuts by 95% the emission of ammonia; described by the EU as one of the main sources of health-damaging air pollution.
On a 200-cow dairy farm this equates to "a reduction of 199 tons of carbon equivalent every year with one machine," said Puttick, adding that they're now looking to scale out the technology across the UK livestock sector, and have recently installed it at a pig farm.

The N2 Applied farm in Buckinghamshire, England.
A commercial model of the device is due for release in June 2022, in a modular "stackable" form; so bigger farms can add units to cope with their amount of slurry. Exact pricing is yet to be announced, but Puttick said capital investment for a farm will be similar to that of a medium-sized tractor.
N2 Applied has received over 17 million euros (around US $19.2 million) of funding from the European Union's Horizon 2020 research and innovation program.
The Global Methane Pledge, launched at the COP26 summit in Glasgow in November, committed to reducing methane by 30% by 2030.
Methane has a higher heat-trapping potential than CO2 but it breaks down in the atmosphere faster, meaning deep cuts in methane emissions by 2030 could have a rapid impact on slowing global warming.
A UN report in May said steep cuts in methane emissions this decade could avoid nearly 0.3 degree Celsius of global warming by the 2040s.

Hyundai backs hydrogen powered cars despite being a decade behind EVs

December 1, 2021 2 By BRET WILLIAMS

The company feels that battery electric technology is far ahead, but hydrogen cars are still worth pursuing.

Hyundai has announced that while it believes that H2 vehicles remain a decade behind their battery electric counterparts, it is still worthwhile to invest in both zero-emission technologies.
The company still plans to continue in the electric and fuel cell vehicle marketplaces.

Hyundai Motor is investing in electric vehicles (EVs) but is also moving forward with both hydrogen powered cars and heavy-duty trucks. Its first electric hatchback will be on its way to the United States in the next few weeks. Moreover, the automaker also unveiled a battery electric SUV last month in Los Angeles.

That said, even as it starts to roll out new electric vehicles, the Korean automaker also has intentions to bring hydrogen cars into the mainstream. Still, it doesn’t expect H2 vehicles to be the most competitive vehicles until closer to 2030.
Hyundai has already said the system in its hydrogen powered cars and trucks is twice as powerful.

The H2 fuel cell vehicles will not only be twice as powerful as its current version but is also 30 percent smaller and will cost half as much. At the same time, José Moñoz, Hyundai chief operating officer and head of its operations in the Americas said that hydrogen cars remain at about the same point in development that battery electric vehicles had reached in the early 2010s.

“At that time people were still asking, ‘Is this going to happen? This is not true. We don’t have infrastructure. People won’t like it.’ Now there’s (charging) infrastructure; the technology has evolved; the ranges are better; the features are great. And more importantly, people who buy one now say they’ll buy another,” said Moñoz in a recent Forbes report discussing the automaker’s hydrogen powered cars. “Hydrogen is going through a similar phase—the phase of introducing a new technology. But we need better (fueling) infrastructure because it’s still very limited. However, in terms of the reaction by the consumer, when they drive a vehicle that is powered by hydrogen, there is a fantastic reaction.”

Interested in alternative energy and how hydrogen fuel works?
Many are wondering…is hydrogen energy the future? There are many signs that point to yes…someday, the world could rely on H2 to keep the lights on – Learn more about How efficient is a hydrogen fuel cell. Also, why big named companies like Rolls Royce, Shell, BP and more investing into green hydrogen projects for the near future – Read more about – Who is the largest producer of green hydrogen? Also, make sure to visit our H2 Learning Center.

US Hydrogen Fuel Cell Powered Ferry Completes First Fueling

first hydrogen fueling for U.S. fuel cell ferry Sea Change — Sea Change was fueled from a truck in Washington (Swtich Maritime)

In the race to develop and operate hydrogen fuel cells for commercial vessels, the U.S. effort known as the Sea Change, a catamaran ferry to operate in San Francisco Bay, reports that it has achieved additional key milestones. The vessel, which was launched in August, has completed its first fueling with hydrogen gas for a vessel in the United States and has received critical approvals as it continues on track to enter service in 2022.

Switch Maritime, which built the vessel as the first in a series it plans to develop with hydrogen propulsion, reported that the Sea Change completed its first hydrogen fueling. At All American Marine shipyard in Bellingham, Washington, the Sea Change received hydrogen into its 242 kg tanks on the upper deck. The fueling during sea trials is being handled by West Coast Clean Fuels, which Switch retained to develop and permit the end-to-end fuel supply chains that will deliver hydrogen to the Sea Change, as well as BayoTech, for high-pressure gaseous hydrogen delivery using transport trailer-to-ship transfer to Sea Change during sea trials in Washington.

The Sea Change uses a first-of-its-kind maritime hydrogen and fuel cell system designed and developed by Zero Emission Industries. The company also developed the system demonstrated during the fueling on November 18 that allows the vessel to receive gaseous hydrogen directly from a hydrogen truck. The fuel loaded in the vessel’s tanks included green hydrogen, produced in California by an electrolyzer powered with renewable solar power.

“While it’s taken us years to get to this point, the timing couldn’t be better,” says Pace Ralli, CEO of Switch Maritime. “In this moment, our nation is more committed than ever to making the transition to a carbon-free economy. Hydrogen will play a major role in that future, and major players in the maritime industry are ready to decarbonize. We are grateful to all our partners, and proud to play a small role in accelerating the widescale adoption of hydrogen power. Hopefully this is just the first domino to fall.”

The fueling follows the regulatory approval in October by the United States Coast Guard of the hydrogen powertrain and storage systems onboard the Sea Change, representing the culmination of years of cooperation with the USCG focused on safely integrating hydrogen power and storage systems on passenger vessels. According to the companies, the achievement of this significant milestone they believe will unlock the possibility of many future deployments of similar hydrogen power systems on all vessel types – including ocean-going containerships.

The new 75-passenger ferry, which is a 70-foot catamaran ferry designed by Incat Crowther, is equipped with a hydrogen fuel cell system from ZEI. The system includes 360kW of fuel cells from Cummins and 242kg of hydrogen storage tanks from Hexagon Purus. A 600kW electric propulsion system from BAE Systems includes 100kWh of lithium-ion battery storage from XALT. It was built at All American Marine and launched in August.

The Sea Change is unique in that it uses gaseous hydrogen in its fuel cell. Other demonstrate vessels are burning liquid hydrogen in a more traditional combustion engine. Switch says the Sea Change will use the hydrogen in fuel cells producing electricity to power electric motors for distances up to 300 nautical miles and speeds up to 20 knots. That will give the vessel similar capabilities to similar diesel-powered vessels.

Having successfully performed the first hydrogen fueling, the Sea Change is now performing final operational sea trials before delivery from the shipyard and before starting operations in the California Bay Area in Q1 2022.

Switch’s vision is to achieve a fully zero-carbon fueling supply chain of green hydrogen, which is currently in short supply in the U.S. Building more and larger vessels that demand large volumes of hydrogen offtake the company believes will increase green hydrogen production volumes, and drive the cost of hydrogen lower than diesel, further advancing the rollout of hydrogen-fueled fleets.

Leading Towboat Owner Plans to Buy a Fuel Cell-Powered Prototype

Maritime Partners, a leading vessel owner and financier in the inland towing sector, is planning to order a prototype methanol-fueled, fuel-cell-powered towboat for delivery in 2023.

The boat will be built to a novel design developed by the naval architects at Elliott Bay Design Group (EBDG), in partnership with system integrator ABB and methanol-to-hydrogen supplier E1 Marine. The combination of methanol fuel, E1's methanol reformer (which strips out the methanol's hydrogen) and a hydrogen fuel cell gives it a significant edge over battery-powered systems for sheer range. The system delivers about 550 miles of transit distance - enough for about four days of travel - for a typical towboat running at normal speeds.

EBDG thinks that this combination may be the only commercially-available option for decarbonizing a towboat for long-haul operations. Finding a new power source for the towboat sector is difficult, since towboats have limits for size and displacement in order to fit under bridges and navigate shallow rivers. Batteries only work on fixed routes, with daily time and access for charging, and a towboat’s limited storage capacity restricts the use of pressurized or cryogenic gases as fuels. There are also very few dockside facilities that can bunker a towboat with these more technically-demanding fuels, and as a practical matter, this would limit a vessel’s range and functionality. By contrast, methanol is a ubiquitous industrial chemical and a familiar cargo for the inland towboat industry.

"The US towboat market is one of the most traditional in the world, so it's important to recognise what this represents: the first step in a shift from diesel electric to methanol electric, and a major advancement towards zero emissions," said David Lee of ABB Marine & Ports.

Virtually all methanol on the market today is derived from natural gas, and while its use does result in carbon emissions, the higher efficiency of a fuel cell means that operating the new system would result in a lower carbon footprint than operating a conventional diesel engine. According to E1, while running on standard methanol the hydrogen generator / fuel cell set produces zero particulates, zero NOX, zero SOX, and 28 percent less CO2 than a diesel generator. If the operator switches to "green" methanol produced from a source of green hydrogen - when and if it becomes available - this carbon footprint could be further reduced without altering the equipment on board.

“Shipowners have been understandably reluctant to commit to low carbon fuels until the infrastructure is available to refuel their vessels. The M/V Hydrogen One solves that problem by using methanol, which is safe and readily available worldwide," said Austin Sperry, the co-founder and COO at Maritime Partners.

Facebook sold ads that compared vaccines to the Holocaust and said 'Make Hanging Traitors Great Again'

mloh@businessinsider.com (Matthew Loh)

A man looks at a computer screen with a Facebook logo in Warsaw, Poland on February 21, 2021

Jaap Arriens/NurPhoto via Getty Images

Facebook made $780,000 selling ads with violent and anti-vaccine messages, CNN's Donnie O'Sullivan reported.

It boosted at least four ads for shirts that compared vaccines to the Holocaust.
The pages running the ads have fewer than 10,000 followers, but the ads reached around 1 million people each.

Facebook sold ads for t-shirts and sweaters with slogans that likened the US COVID-19 response to Nazi Germany and suggested that vaccines are poison or like the Holocaust, CNN's Donnie O'Sullivan reported.

In the last few years, the social media platform has made $780,000 in total from such clothing ads, which were run by the pages "Ride the Red Wave" and "Next Level Goods," Sullivan wrote.

"Slowly and quietly, but it's a Holocaust,"

read the shirt design on one ad, which featured a syringe alluding to the COVID-19 vaccine.

Another ad touted a similar syringe design on a shirt that said: "Proudly Unpoisoned." According to Facebook data, it was mostly shown to men, and the top states it displayed the ad in were Texas, Florida, Pennsylvania, and California.

On November 29 to 30, the page "Ride the Red Wave" ran ads for a sweater that said: "I'm originally from America but I currently reside in 1941 Germany," comparing the US pandemic response to the Nazi regime's rule of Germany in the early years of World War II.

"Make Hanging Traitors Great Again," said another shirt on an ad run in June. While the first three ads were taken down for violating Facebook's advertising policies, this one has not been removed at the time of publishing.

The pages running these ads paid Facebook to reach estimated audiences of more than 1 million people per ad, though "Ride the Red Wave" has fewer than 10,000 followers, according to CNN, and "Next Level Goods" has fewer than 7,000 likes, according to Facebook data.

A spokesperson for Facebook's parent company, Meta, told CNN that the ads comparing vaccines to the Holocaust and poison, as well as the one that suggested the pandemic response was like 1941 Germany, went against Facebook's vaccine misinformation policies.

It did not say if the "Make Hanging Traitors Great Again" ad violated its policies, per CNN.

Facebook and Meta regularly say that they've aided vaccination efforts and have helped people get accurate and verified information about COVID-19.

Facebook did not immediately respond to Insider's request for comment.

REST IN POWER

Kentucky author and 'Merry Prankster' Ed McClanahan dies

LEXINGTON, Ky. (AP) — Ed McClanahan, a Kentucky author, teacher and friend of counterculture icon Ken Kesey, died Saturday at his home in Lexington, according to his wife. He was 89.

© Provided by The Canadian Press

McClanahan lived in Lexington with his wife Hilda, who remembered him as a “great man.”

“Everybody knows what an icon he was," she said Wednesday. “I miss him.”

McClanahan was born in Brooksville in Bracken County. In 1962, he met Kesey, author of “One Flew Over the Cuckoo’s Nest,” and Kesey’s band of Merry Pranksters while at Stanford University as part of a creative writing fellowship, according to the Lexington Herald-Leader.

The communal travelers' exploits were chronicled in Tom Wolfe’s 1968 book “The Electric Kool-Aid Acid Test.” When he was with the LSD-fueled jesters, McClanahan was known as “Captain Kentucky" and would frequently wear costumes, an experience he recalled in his 1985 memoir, “Famous People I Have Known.”

McClanahan's first book, a coming-of-age novel entitled “The Natural Man,” was published in 1983, and McClanahan was inducted into the Kentucky Writers Hall of Fame in 2019. His last two books were published last year. His cause of death was not reported.

“Ed was one of the best writers of my time,” a friend of McClanahan’s, Kentucky author Wendell Berry, told the newspaper. “He was almost perfect in the way he made his sentences, the way he heard his sentences. He had a very large sense of humor and it came to rest on his language.”

McClanahan also taught writing at multiple universities, including Stanford University, Oregon State University, the University of Kentucky, Northern Kentucky University and the University of Montana.

Frank X. Walker, the director of the University of Kentucky Creative Writing Program, told the Herald-Leader that he was saddened to lose “someone who had made so many of us laugh so hard for so long."

“Ed was a pillar in the community of writers of his generation that established Lexington and Kentucky as a legitimate literary hotbed,” Walker said. “His mentorship and support of a whole generation of younger writers will be missed.”

The Associated Press

LA REVUE GAUCHE - Left Comment